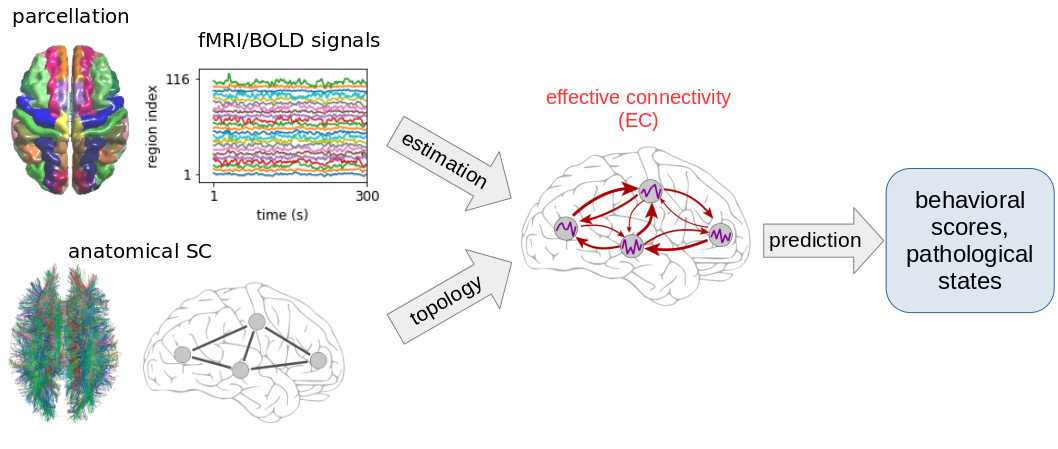
A main focus of my post-doc time in Barcelona was on the analysis of functional magnetic resonance imaging (fMRI) data and interpret it in terms of brain communication. This relies on a whole-brain dynamic model fitted to the fMRI signals to reproduce their propagation pattern, which provides an estimation for the directional interactions between brain regions at the single session level. The latter correspond to the concept of effective connectivity (EC) and aim to go beyond a simple phenomenological description of the empirical signal correlations (functional connectivity, FC). In particular, EC can be constrained by anatomical data (or structural connectivity, SC) such that EC describes the strength modulation of cortico-cortical fibers, lumping together biological mechanisms like synaptic efficacy or local excitability. EC provides a robust signature (or biomarkers) to decode cognitive or pathological states and can be further analyzed using network theory to identify e.g. functional communities of brain regions.
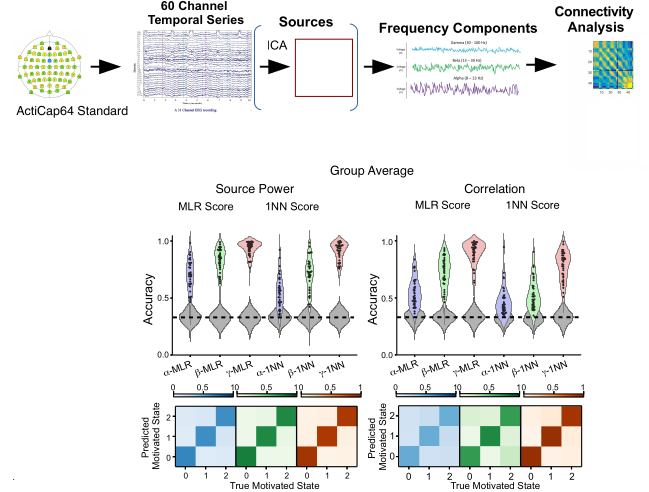
I have started to transpose this framework to interpret spiking activity at the microscopic level and electro/magneto-encephalographic (EEG/MEG) data at the meso/macro-scopic level (including intracranial EEG). The first step is to understand where "information" (understood colloquially here) related to e.g. behavioral conditions is embedded in the signals, in particular distributed across brain rhythms like alpha, beta and gamma. The second step is to adapt the design of the dynamic model to match the relevant spatio-temporal structure of the empirical signals.
I also plan to formally compare my gradient-descent methods (focused on single-trial estimation) with the Bayesian estimation framework and Granger causality analysis, as well as the estiamtion of time-resolved EC to capture the dynamics of neuronal interactions during trials.
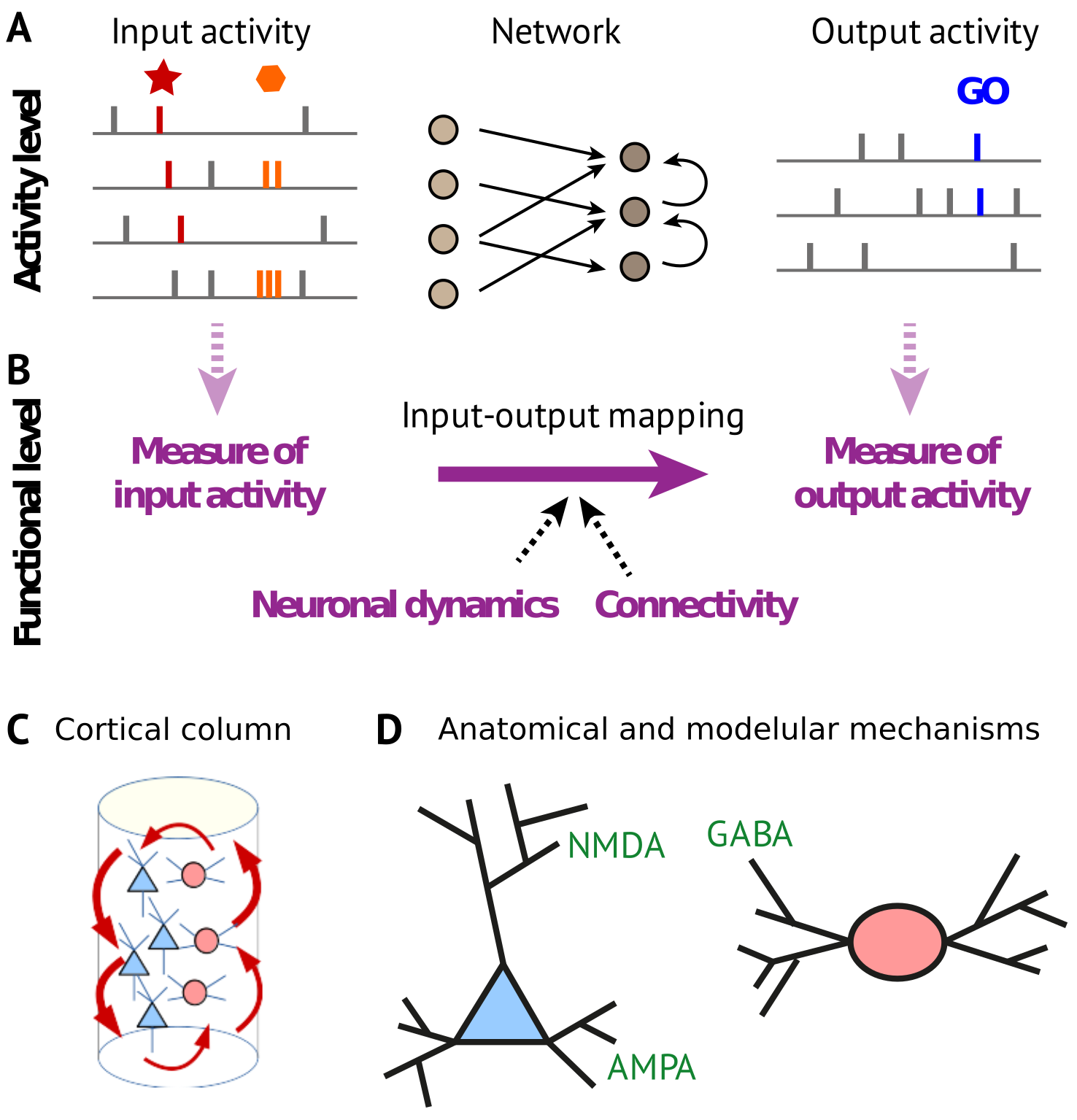
I am interested in neuronal processing in networks, in particular involving recurrent connectivity. I first studied unsupervised models like spike-timing-dependent plasticity (STDP), but recently switched to supervised learning with the covariance perceptron (for non-spiking neurons so far). Both rely on the assumption that neuronal representations, here understood as activity patterns that form the basis of information to be processed, is embedded in statistics of signals, like pairwise covariances for order 2. This aims to go beyond representations based on spiking rates as orientation tuning curves for the early visual system.
Mathematical modeling formalizes the input-output mapping implemented by the network dynamics, which is shaped by learning. Recurrent connectivity implies further non-linearities due to the network feedback, yielding an intricate relationship when combined with learning dynamics.